Definition
Eine kubische Funktion enthält ein x3 mit 3 als höchster Potenz von x; die allgemeine Form ist:
$$f(x) = ax^3 + bx^2 + cx + d$$
Dabei darf a nicht 0 sein (sonst würde der kubische Term verschwinden); b, c und d hingegen können 0 sein, dann fallen diese Terme weg.
Alternative Begriffe: Funktion 3. Grades, Funktion dritten Grades.
Beispiel
Eine kubische Funktion sei $f(x) = x^3 - 3x^2 + 2x$
Auf die allgemeine Form bezogen ist hier a = 1, b = -3, c = 2 und d= 0.
Nullstellen
Um die Nullstellen einer kubischen Funktion zu bestimmen (also die x-Werte, für welche die Funktion f(x) den Wert 0 annimmt), wird diese gleich 0 gesetzt:
$$f(x) = x^3 - 3x^2 + 2x = 0$$
Kubische Gleichungen werden in der Regel über einen Umweg gelöst: sie werden in eine quadratische Gleichung überführt und diese kann dann mit den bekannten Lösungswegen (abc-Formel, p-q-Formel, Quadratische Ergänzung) gelöst werden.
Die Überführung in eine quadratische Gleichung kann mit der Polynomdivision erfolgen (siehe das dortige Beispiel für die obige Funktion) oder mit dem Horner-Schema.
Dazu muss jedoch zunächst eine Nullstelle bekannt sein – oder geraten werden; bei der obigen Funktion sieht man leicht, dass bei x = 0 eine Nullstelle liegt und damit lässt sich die Polynomfunktion beginnen (weitere Nullstellen sind dann 1 und 2).
Bei der Beispielfunktion geht es noch einfacher, indem man x einfach ausklammert: $f(x) = x \cdot (x^2 - 3x + 2)$; dann liegt die quadratische Gleichung im zweiten Term $x^2 - 3x + 2$ bereits vor.
Lösen wir die quadratische Gleichung mit der p-q-Formel:
Die p-q-Formel in ihrer allgemeine Form lautet für x2 + px + q = 0:
$$x_{1/2} = \frac{-p}{2} \pm \sqrt {\left (\frac {p}{2}\right)^2 - q}$$
Dabei ist p hier (-3) und q ist 2.
Das gibt dann 2 Lösungen x1 und x2:
$$x_1 = \frac{-(-3)}{2} + \sqrt {\left (\frac {(-3)}{2}\right)^2 - 2}$$
$$= \frac{3}{2} + \sqrt {0,25} = \frac{3}{2} + \frac{1}{2} = 2$$
$$x_2 = \frac{-(-3)}{2} - \sqrt {\left (\frac {(-3)}{2}\right)^2 - 2}$$
$$= \frac{3}{2} - \sqrt {0,25} = \frac{3}{2} - \frac{1}{2} = 1$$
Diese kubische Funktion hat also insgesamt 3 Nullstellen: 0, 1 und 2.
Kontrolle
$$f(0) = 0^3 - 3 \cdot 0^2 + 2 \cdot 0 = 0 - 0 + 0 = 0$$
$$f(1) = 1^3 - 3 \cdot 1^2 + 2 \cdot 1 = 1 - 3 + 2 = 0$$
$$f(2) = 2^3 - 3 \cdot 2^2 + 2 \cdot 2 = 8 - 12 + 4 = 0$$
Bedeutung
Mit dem "Hoch-3-Term" x3 hat man etwas, das wie das Volumen eines Würfels mit gleichen Seitenlängen stark skaliert: ein Würfel mit 10 cm Seitenlänge hat ein Volumen von 103 = 1.000 Kubikzentimeter, ein Würfel mit einer doppelten Seitenlänge von 20 cm Seitenlänge hat bereits ein Volumen von 203 = 8.000 Kubikzentimeter, also das Achtfache.
Kubische Parabel
Der Graph einer kubischen Funktion heißt kubische Parabel.
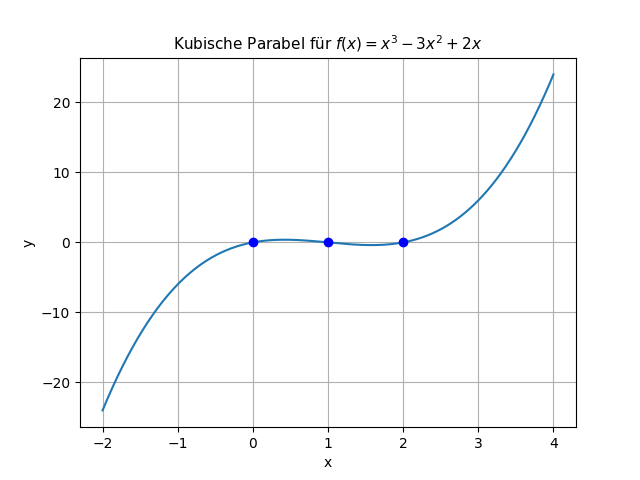
Hier sind die 3 Nullstellen bei x = 0, x = 1 und x = 2 als Punkte auf der kubischen Parabel markiert.
Fazit
- f(x) = a · x3 + b · x2 + c · x + d – a ≠ 0; der Graph ist eine S-förmige Kubikparabel
- Nullstellen: f(x) = 0 setzen; eine Nullstelle erraten oder erkennen, dann per Ausklammern oder Polynomdivision in eine quadratische Gleichung überführen
- Lässt sich x ausklammern (d = 0), ist x = 0 stets eine Nullstelle – die restlichen Nullstellen folgen aus dem quadratischen Faktor
- Alternative Bezeichnungen: Funktion 3. Grades, ganzrationale Funktion dritten Grades
Selbsttest: Kubische Funktion
Aufgabe: Kubische Funktion
Gegeben ist f(x) = 2x3 + 4x2 − 6x.
Bestimmen Sie alle Nullstellen der Funktion.
Ausklammern: f(x) = 2x · (x2 + 2x − 3)
Erste Nullstelle: x1 = 0 (da 2x = 0)
Quadratischer Faktor: x2 + 2x − 3 = 0
p-q-Formel mit p = 2, q = −3: x = −1 ± √(1 + 3) = −1 ± 2
x2 = −1 + 2 = 1 x3 = −1 − 2 = −3
Ergebnis: Die drei Nullstellen sind x1 = 0, x2 = 1 und x3 = −3.