Lineare Funktion
Lineare Funktion Definition
Eine lineare Funktion hat die allgemeine Form:
$$y = m \cdot x + b$$
Statt m und b werden oft auch andere Buchstaben verwendet, statt y auch f(x).
Grafisch ist das eine durch die Geradengleichung $y = m \cdot x + b$ beschriebene Gerade, die
- im Punkt b die y-Achse schneidet (y-Achsenabschnitt bzw. Ordinatenabschnitt) und
- die Steigung m hat.
"Steigung" sollte man nicht zu wörtlich nehmen: für m = 0 ist die Gerade waagrecht und parallel zur x-Achse (steigt also nicht), für m < 0 fällt die Gerade (man sagt dann trotzdem: die Gerade hat eine negative Steigung).
Viele ökonomische Zusammenhänge sind linear.
Beispiel
Ein Internet-Tarif hat eine monatliche Grundgebühr von 20 €; je Megabyte Datenvolumen kommen 2 € dazu.
Als lineare Funktion:
$$y = 2 \cdot x + 20$$
Dabei steht die Variable x für die Anzahl der Megabyte, m ist 2, b ist 20 und y sind die monatlichen Internetkosten in €.
Bei einem Datenvolumen von 0 Megabyte wären die Kosten 2 × 0 + 20 = 20 €.
Bei einem Datenvolumen von 5 Megabyte wären die Kosten 2 × 5 + 20 = 30 €.
Die beiden Daten wären schon ausreichend, um die Gerade durch die beiden Punkte (0, 20) und (5, 30) zu zeichnen.
Die konstante Steigung von 2 bedeutet, dass jedes Megabyte (MB) gleich viel (zusätzlich) kostet.
Mit linearen Funktionen werden also allgemein gleichförmige Verläufe / Entwicklungen beschrieben (1 MB mehr kostet 2 € zusätzlich, 2 MB mehr kosten 4 € zusätzlich, 3 MB mehr kosten 6 € zusätzlich usw.).
Alternative Begriffe: Lineare Funktionsgleichung.
Lineare Funktion zeichnen
Der Graph der obigen linearen Funktion sieht so aus:
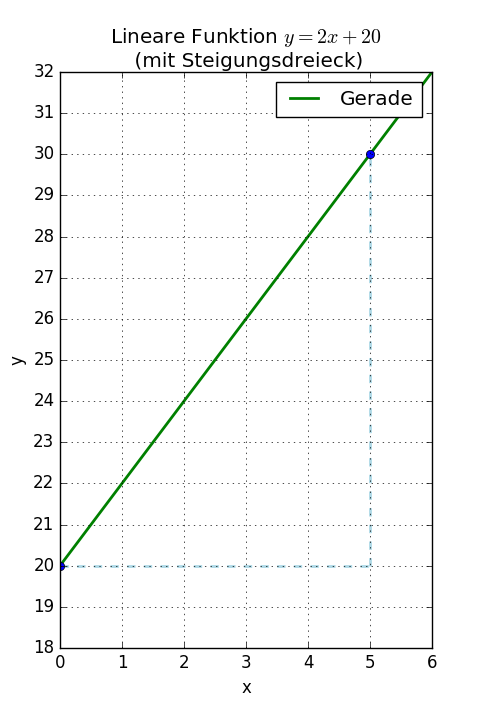
Die gestrichelten Linien stellen das Steigungsdreieck (siehe unten) dar.
Steigung berechnen / Steigungsdreieck
Oben war die Steigung mit m = 2 gegeben. Hat man jedoch nur die Gerade und soll die Steigung berechnen, geht das mit 2 beliebigen Punkten auf der Gerade.
Beispiel: Steigung berechnen
Wir nehmen die 2 Punkte von oben:
$$(x_1, y_1) = (0, 20)$$
$$(x_2, y_2) = (5, 30)$$
Dann werden die Differenzen der y-Werte gebildet und durch die Differenzen der x-Werte geteilt:
$$m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{30 - 20}{5 - 0} = \frac{10}{5} = 2$$
Die Steigung wird also in Einheiten gemessen: eine Einheit nach rechts bedeutet 2 Einheiten nach oben (bei Verkehrsschildern wäre diese Steigung in Prozent: 200 %).
Ist der errechnete Wert negativ, liegt eine negative Steigung (ein Gefälle) vor (mehr von x führt zu weniger von y).
Ist die Steigung 0, ist die Gerade waagrecht.
Steigungsdreieck
Zeichnet man die senkrechte Differenz (der y-Werte, also 10 Einheiten) vom zweiten Punkt ausgehend nach unten und die waagrechte Differenz (der x-Werte, also 5 Einheiten) vom ersten Punkt ausgehend nach rechts ein, bilden diese zusammen mit dem Geradenabschnitt das sogenannte Steigungsdreieck.
Steigungswinkel
Das Steigungsdreieck hat einen Steigungswinkel; wenn man diesen mit $\alpha$ bezeichnet, entspricht die Steigung m dem Tangens von $\alpha$:
$$tan(\alpha) = \frac{Gegenkathete}{Ankathete} = \frac{10}{5} = 2$$
Der Steigungswinkel ist ca. 63,435 Grad (Taschenrechner: 2 und TAN-1 drücken).
Punktsteigungsform
Alternativ kann die Geradengleichung auch in der Punkt-Steigungs-Form bzw. Punkt-Steigungs-Formel geschrieben werden, wenn man die Steigung und einen Punkt auf der Geraden hat.
Beispiel: Punktsteigungsform
Wir nehmen die Steigung m = 2 und den zweiten Punkt von oben: $(x_2, y_2) = (5, 30)$.
Die Punktsteigungsform ist allgemein (mit p für den Punkt):
$$y = m \cdot (x - x_p) + y_p$$
Mit den Werten:
$$y = 2 \cdot (x - 5) + 30$$
Wenn man das weiter führt, kommt man wieder zur Normalform der Geradengleichung:
$$y = 2 \cdot x - 2 \cdot 5 + 30$$
$$y = 2x - 10 + 30$$
$$y = 2x + 20$$