Zweite Ableitung

Beispiel: 2. Ableitung bilden

Für die Potenzfunktion f(x) = x³ ist die 1. Ableitung f'(x) = 3x².

(Bei der Ableitung einer Potenzfunktion wird der Exponent (hier: 3) als Faktor vor den Term gezogen und die Potenz wird um 1 verringert (hier: von 3 auf 2).)

Leitet man diese 1. Ableitung erneut ab, erhält man die 2. Ableitung f''(x) = 6x.

(Wieder die Ableitung einer Potenzfunktion: Exponent (hier: 2) als Faktor vor den Term ziehen (hier: 2 × 3 = 6) und die Potenz um 1 verringern (hier: von 2 auf 1; und x¹ entspricht x).)

Bedeutung der 2. Ableitung

Die 2. Ableitung hat 2 Bedeutungen bzw. Nutzen:

1. Bedeutung: zeigt Krümmung an

Die 2. Ableitung (bzw. ihr Vorzeichen) zeigt, wie die Funktion (an einer Stelle) gekrümmt ist:

• 2. Ableitung f''(x) > 0: die Kurve ist konvex bzw. linksgekrümmt (man kann sich eine Hängebrücke vorstellen); an der Stelle x = 3 zum Beispiel wäre die Funktion wegen f''(3) = 6 × 3 = 18 > 0 konvex. Eine Sekante durch 2 Punkte der Kurve würde dann oberhalb der Kurve verlaufen (so wie ein Baumstamm, den man zwischen die beiden Brückenpfeiler der Hängebrücke legt).
• 2. Ableitung f''(x) < 0: die Kurve ist konkav bzw. rechtsgekrümmt (man kann sich einen Regenbogen vorstellen); an der Stelle x = -3 zum Beispiel wäre die Funktion wegen f''(-3) = 6 × (-3) = -18 < 0 konkav. Eine Sekante durch 2 Punkte der Kurve würde dann unterhalb der Kurve (des Regenbogens) verlaufen.

Die 2. Ableitung f''(x) = 6x ist für alle x > 0 auch größer 0, sie ist für alle x < 0 ebenfalls < 0. Die jeweilige Krümmung im positiven und negativen x-Bereich kann man in der Grafik gut sehen:

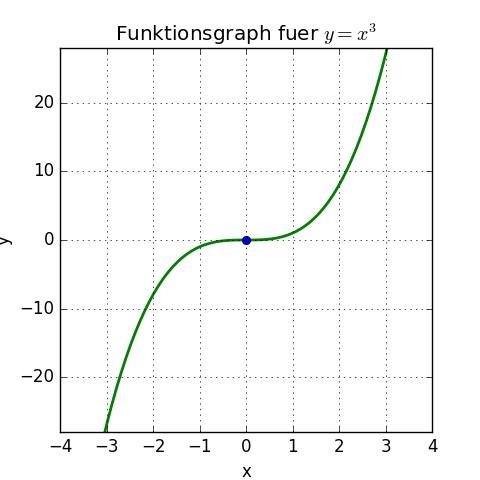
2. Bedeutung: definiert kritische Punkte

Hat man mit der 1. Ableitung einen kritischen Punkt bestimmt, bei dem die 1. Ableitung = 0 ist (das wäre bei f'(x) = 3x² bei x = 0 der Fall), kann man mit der 2. Ableitung bestimmen, ob in diesem Punkt ein Sattelpunkt, ein Wendepunkt, ein Maximum oder ein Minimum (Extremwerte) vorliegt (in der Grafik oben liegt ein Sattelpunkt vor: ein Wendepunkt an der Stelle x = o, in dem die Steigung 0 ist).

Zweite, dritte, vierte und so weiter Ableitungen werden höhere Ableitungen genannt.

Bei einfachen Funktionen wie zum Beispiel linearen Funktionen ist schnell Schluss mit höheren Ableitungen. Die Funktion f(x) = 2x beispielsweise ist einmal abgeleitet f'(x) = 2. Diese Konstante, welche die Steigung der Geraden angibt, ergibt bei einer weiteren Ableitung f''(x) = 0, das heißt die Steigung ändert sich nicht (die Steigung ist überall gleich). Höhere Ableitungen bringen einen hier nicht weiter.