Grenzrate der Substitution
Definition
Die Grenzrate der Substitution gibt an, in welchem Verhältnis Gut 1 und Gut 2 getauscht werden, ohne dass sich der Nutzen des Haushalts / Konsumenten ändert.
Sie wird oft abgekürzt mit GRS oder mit MRS für die englische Bezeichnung Marginal Rate of Substitution.
Grundidee
Substituieren heißt das eine gegen das andere ersetzen oder austauschen:
Adam sitzt im Kino mit 2 Portionen Popcorn und 4 Bechern Limonade; wir nehmen an, wir können seine Zufriedenheit messen oder abfragen, sie beträgt 6 (auf einer Skala von 0 bis 10).
Wenn Adam nun beispielsweise bereit ist, 2 Becher Limonade gegen eine weitere Portion Popcorn zu tauschen und damit gleich zufrieden ist (er hat jetzt 3 Popcorn und 2 Limonaden), ist das an diesem Punkt die Grenzrate der Substitution, also das Austauschverhältnis von 1 zu 2 zwischen Popcorn und Limonade, das ihn gleich zufrieden lässt.
Beispiel
Formel
Die Grenzrate der Substitution berechnet sich als Quotient aus dem Grenznutzen von x (Gut 1) und dem Grenznutzen von y (Gut 2), mit einem negativen Vorzeichen versehen.
GRS = - (MU1 / MU2)
Nutzenfunktionen
Aufbauend auf dem Beispiel zur Nutzenfunktion: diese war
U (x, y) = x + 3 × y
- mit x für die konsumierte Menge von Gut 1 (Liter Milch) und
- mit y für die konsumierte Menge von Gut 2 (kg Brot).
Berechnung
Der mit MU1 (MU für Marginal Utility) bezeichnete Grenznutzen von Gut 1 entspricht der 1. Ableitung der Nutzenfunktion nach x, das ergibt 1.
Wenn man die Funktion U (x, y) = x +3 × y partiell nach x ableitet, ergibt der erste Summand x abgeleitet nach x dann 1 und der zweite Summand 3 × y ergibt abgeleitet nach x dann 0 (aus Sicht von x ist der Term eine Konstante), in Summe also 1 + 0 = 1.
Der mit MU2 bezeichnete Grenznutzen von Gut 2 entspricht der 1. Ableitung der Nutzenfunktion nach y, das ergibt als partielle Ableitung 3.
Die Grenzrate der Substitution MRS = - (MU1 / MU2) ist damit -1/3.
Interpretation
Es handelt sich hier um eine konstante Grenzrate der Substitution, da sie nicht von x oder y abhängt. Der Konsument ist also bei dieser Nutzenfunktion immer bereit, in einem konstanten Verhältnis 1 zu 3 zu tauschen.
Ein Liter Milch und 1 kg Brot – mit dem Nutzen U (1, 1) = 1 + 3 × 1 = 4 – sind ihm genauso lieb, wie 4 Liter Milch und kein Brot mit dem Nutzen U (4, 0) = 4 + 3 × 0 = 4 oder andere Güterbündel mit demselben Nutzen. Er tauscht jederzeit ein kg Brot gegen 3 Liter Milch.
Grafisch ist die Grenzrate der Substitution die Steigung der Indifferenzkurve, also der Kurve, die grafisch alle Güterbündel (modellhaft bestehend aus 2 Gütern) darstellt, die vom Haushalt / Konsumenten gleichgewertet werden, das heißt ihm den gleichen Nutzen bringen bzw. ihm gleich lieb sind; diese Indifferenzkurve ist in dem vorliegenden Fall eine Indifferenzgerade:
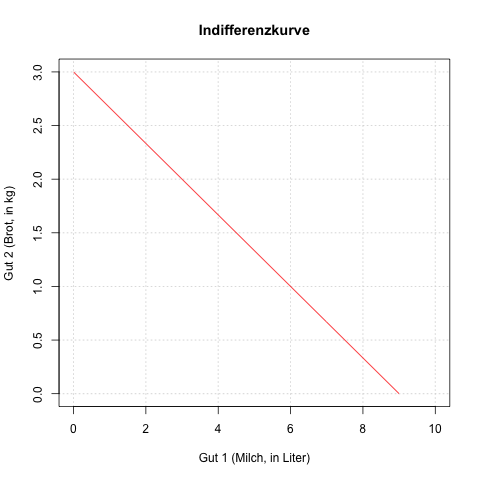
Wofür gut?
Mit der GRS und der Budgetrestriktion kann dann das Haushaltsoptimum – in dem der Nutzen des Haushalts unter Beachtung des Budgets am größten ist – berechnet werden. Das ist das Güterbündel, das dem Haushalt bei seinem verfügbaren Einkommen am meisten (Nutzen) bringt und damit für ihn optimal ist.
Das Zweite Gossensche Gesetz sagt, dass im Haushaltsoptimum die Grenzrate der Substitution dem Verhältnis der Preise der beiden Güter entspricht.